MANOVA - Endossando IA

 MANOVA - Endossando IA

data imc_dat;

input cat $ imc corr kcal;

cards;

AT 20.2 60.7 3200

AT 21.3 54.8 3100

AT 19.3 49.6 2800

AT 21.1 52.3 3300

SEM 22.4 14.9 2600

SEM 21.9 17.8 2700

SEM 23.8 18.6 3200

SEM 24.1 15.1 3300

SE  27.3 2.5 2700

SE  23.4 4.3 2300

SE  25.2 2.3 2600

SE  26.4 2.6 3200

PR 26.2 4.1 2600

PR 24.2 2.1 2700

PR 25.4 1.9 2650

;

proc print;

run;

proc glm;

 class cat;

 model imc corr kcal  = cat;

 contrast " Atl e Semiat Vs Seden e Prof"  cat 1 -1 -1 1;

 contrast " Professor Vs Sedentario" cat  0 1 -1 0;

 contrast " Atleta Vs Semiatleta" cat -1 0 0 1;

 manova h=_all_ / printe printh;

 contrast " Atl e Semiat Vs Seden e Prof"  cat 1 -1 -1 1;

 contrast " Professor Vs Sedentario" cat  0 1 -1 0;

 contrast " Atleta Vs Semiatleta" cat -1 0 0 1;

run;

Elaboração de Contraste:

AT PR  SE SEM

1  -1 -1   1 Atleta e Semiatleta Vs Professor e Sedentario

0   1 -1   0 Professor Vs Sedentario

1   0  0  -1 Atleta Vs Semiatleta

3  -1 -1  -1  Atleta Vs Outras Categorias

/* 
contrast " Atl e Semiat Vs Seden e Prof"  cat 1 -1 -1 1;
Pega a ordem alfabetica dos niveis dos fatores para os coeficientes
   dos contrastes 
Se colocar o contraste depois do comando MANOVA faz os contrastes univariados 
tambem

*/

Correlação Residual MANOVA:

Partial Correlation Coefficients from the Error SSCP Matrix / Prob > |r|
DF = 11	imc	corr	kcal
imc	1.000000	0.017729 0.9564	0.697770 0.0116
corr	0.017729 0.9564	1.000000	0.132496 0.6814
kcal	0.697770 0.0116	0.132496 0.6814

Outro Exemplo de Contrastes, Ordem Alfabética:





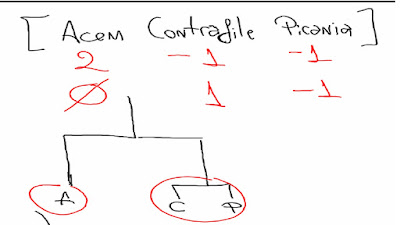
- Análise Multivariada Exemplos: 

Comparar resultados ANOVA com Kruskal-Wallis.

data imc_dat;

input cat $ imc corr kcal;

cards;

AT    20.2  60.7  3200

AT    21.3  54.8  3100

AT    19.3  49.6  2800

AT    21.1  52.3  3300

SEM   22.4  14.9  2600

SEM   21.9  17.8  2700

SEM   23.8  18.6  3200

SEM   24.1  15.1  3300

SE    27.3  2.5   2700

SE    23.4  4.3   2300

SE    25.2  2.3   2600

SE    26.4  2.6   3200

PR    26.2  4.1   2600

PR    24.2  2.1   2700

PR         25.4         1.9        2650

;

proc print;

run;

proc npar1way data=imc_dat wilcoxon dscf;

 class cat;

 var imc corr kcal = cat;

run;

Tem um erro nesse programa, onde esta? Compare com os slides apresentados antes do programa SAS (Dois slides de Kruskal Wallis com trechos de programa SAS).

 var imc corr kcal = cat; ==> ANOVA, GLM, MANOVA
 var imc corr kcal;          ==> Kruskal Wallis

Resultados de Kruskal Wallis

Arquivo Word para Download:

Download_K_Wallis

Resultados ANOVA dados brutos, transformados e da Estat. Robusta. Tese doutorado do Gabriel.

Machine Learning Não Supervisionado

Data Crunching e Cluster Analysis

Videoaulas

Videoaula 1

Introdução à Estatística Multivariada e à Inteligência Artificial

https://youtu.be/AQdRiLq9lss

Videoaula 2

Data Crunching - Pivot Tables - Pivot ou Tabela Dinâmica em Excel (Calculo da Matriz de Médias Aritméticas)

https://youtu.be/vhHHc7VxgBk

Videoaula 3

Visual Analytics ou Cluster Analysis ou Elaboração do Dendrograma em Linguagem SAS na Nuvem ( SAS on Demand - Free) 

https://youtu.be/jkpbgtRNZ40

- Pesquisar Data:
                      - Mining
                      - Crunching
                      - Analysis

  Tabela Dinâmica - Excel (Pivot Table ou Paivot ou "Pivot" forma de referenciar em empresas)

 e Cluster Analysis

Estatística Multivariada – Cluster Analysis

Vamos começar a “olhar” com a Estatística (algoritmos matemáticos), de forma multivariada.

Isso é muito familiar para a gente por que nosso cérebro (muito mais poderoso que qualquer computador, 20.000 computadores de ultima geração de 2019) enxerga de forma multivariada.

Como reconhecemos os objetos ou as pessoas, por somente um item? Por exemplo, como reconhecemos uma pessoa: sexo, altura, cor do cabelo, formato do rosto, timbre da voz, sotaque, perfume que utiliza (ou que não utiliza), etc.

Na verdade utilizamos todos esses dados e muitos mais simultaneamente, ou seja, nosso sistema de reconhecimento natural é multivariado (como a Estatística Multivariada).

Como nosso cérebro processa toda essa informação em frações de segundo não sabemos. A neurociência está quebrando cabeça com isso. Podemos perguntar para Nicolelis (o neurocientista que dizem ter a maior chance de conseguir um Premio Nobel para o Brasil).

O que podemos fazer com a matemática, estatística e computação é simular de alguma forma primitiva o funcionamento do cérebro.

Esse tipo de abordagem é utilizado nas áreas de Inteligencia de Negócios (BI), Sistemas de Informação ( Data Mining, Data Crunching, Decision Support Systems-DSS e Big-Small Data) e Pesquisa Cientifica

Também é utilizado numa área da Inteligência Artificial denominada Visual Analytics, vejamos o seguinte exemplo, como poderíamos enxergar em dimensão 78?

No exemplo a ser apresentado (arquivo de Excel para download), temos 4 categorias de pessoas: Atletas, Semi-atletas, Sedentários e Professores da ESALQ. Nessas pessoas foram medidas 3 variáveis, Índice de Massa Corporal, Quantos quilômetros corre ou anda por semana e Quilocalorias que Ingere por Dia (modelo trivariado, se tem mais do que uma já é multivariado).

Exemplo para Download:

Exemplo Excel Download

Aqui apresentamos o nosso objetivo, elaborarmos um dendrograma, que é a representação gráfica da saída do procedimento Cluster Analysis do Programa SAS:

                         
                           Tabela Dinâmica
                              em   Excel
                             ( Pivot Table )

Podemos ver nesse exemplo que temos vários representantes de cada categoria, são exatamente 4 (ou quatro repetições de cada categoria)

Para aplicarmos Cluster Analysis devemos calcular previamente as medias aritméticas de cada categoria, para cada uma das 3 variáveis de resposta.

Vamos colocar a sequencia de passos para obtermos essas medias utilizando um recurso muito poderoso de bancos de dados do Excel (tal vez o mais poderoso):

 Tabela Dinâmica ou Pivot Table ou Pivot.

Passo 1 – Marcar o banco de dados original

Passo 2 – Entrar em Inserir e Depois em Tabela Dinâmica.

Passo 3 – Dar OK. Entraremos no Ambiente de Trabalho da Tabela Dinâmica:

Passo 4 – Clicar em Categorias “Cat.”(sem soltar o mouse, operação “Drag”) e arrastar as categorias para o local Rótulos de Linha.

Passo 5 – Arrastar as 3 variáveis observadas: IMC, Corr e Kcal para o local Somatória de Valores (Σ valores). Veja que o protótipo da Tabela Dinâmica, já está pronto, no canto superior esquerdo.

Passo 6 – O problema é que temos somatória dos valores e precisamos de medias aritméticas para entrar no Programa de 

Cluster Analysis do SAS. Como fazer para trocar 

somatória para medias?:


Veja que os dados são de soma, um IMC de 100, praticamente não existe ( 81,9 ; 100,7 ...)

·       Colocar o cursor na célula “soma de IMC”

    ·   Pressionar o botão direito do mouse

·       Escolher a opção: “Configurações do Campo de Valor”

·       Veja que está em “Soma”, clicar em “Média”. 

Veja que agora temos Média de ICM para cada categoria.

·       Fazer mesma operação para Corr e Kcal.

Fim do calculo das medias de cada categoria.

Agora é somente copiar e colar no SAS.

Programa SAS para Cluster Analysis dos Dados Calculados no Excel:

data  pessoas;

input cat $ imc corr kcal;

cards;

DADOS DO SAS DEPOIS DE APLICAR TABELA DINAMICA

;

proc cluster data=pessoas outtree = arvore method = average;

var imc corr kcal;

id cat;

run;

PROC TREE DATA = arvore;

RUN;